Les projections cartographiques : représenter l’impossible
Comment aplatir la Terre ? Cette question, en apparence absurde, est au cœur de la cartographie. Car représenter un globe tridimensionnel sur une feuille plane est un exercice complexe, toujours imparfait. Que ce soit pour l’école, la navigation ou l’analyse spatiale, les cartes sont partout. Et derrière chaque carte, même celles de Google Maps, se cache une projection cartographique, c’est-à-dire une méthode de transformation qui choisit quoi préserver et quoi sacrifier.
Les grands types de projections
Les projections sont souvent classées selon la surface géométrique utilisée pour « projeter » la Terre :
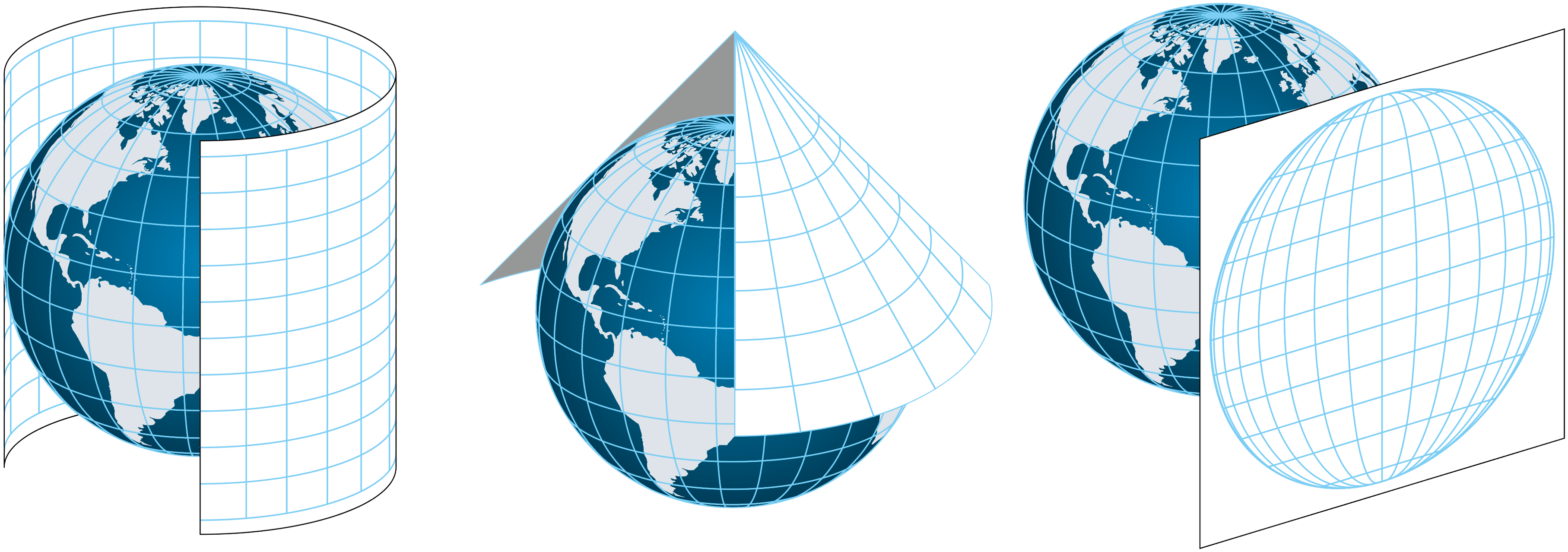
Projection cylindrique : Comme si l’on enroulait un cylindre autour du globe, tangent à l’équateur ou à un autre parallèle.
Projection conique : La Terre est projetée sur un cône qui touche un ou deux parallèles (ex : Lambert conforme).
Projection plane (azimutale) : La projection se fait sur un plan tangent à un point, souvent centré sur un pôle.
Il existe également des projections de compromis pour atténuer visuellement les déformations.
Les types de déformations
On ne peut pas tout représenter correctement sur une carte plane. Il faut choisir entre quatre grandes propriétés géographiques :
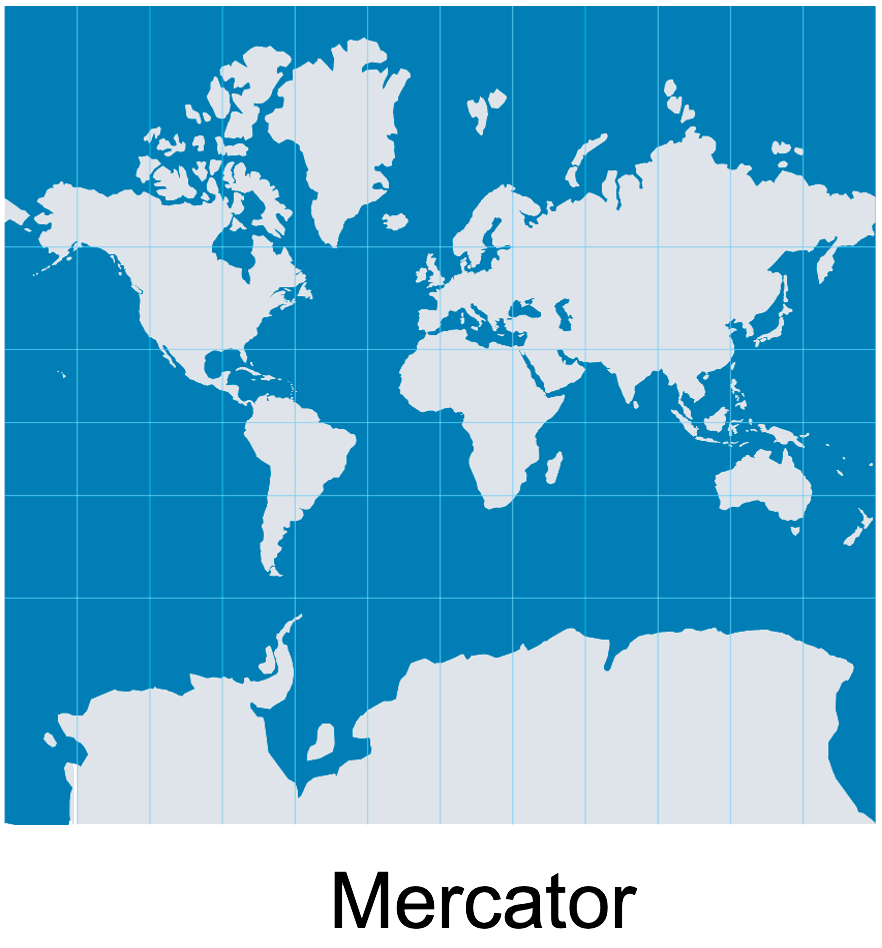
Conformité (Mercator)
Conserve les formes locales et les angles
Préserve fidèlement les formes des objets à petite échelle, grâce au respect des angles locaux
- Idéal pour les cartes côtières, marines, topographiques
- Les surfaces peuvent être très exagérées, surtout près des pôles
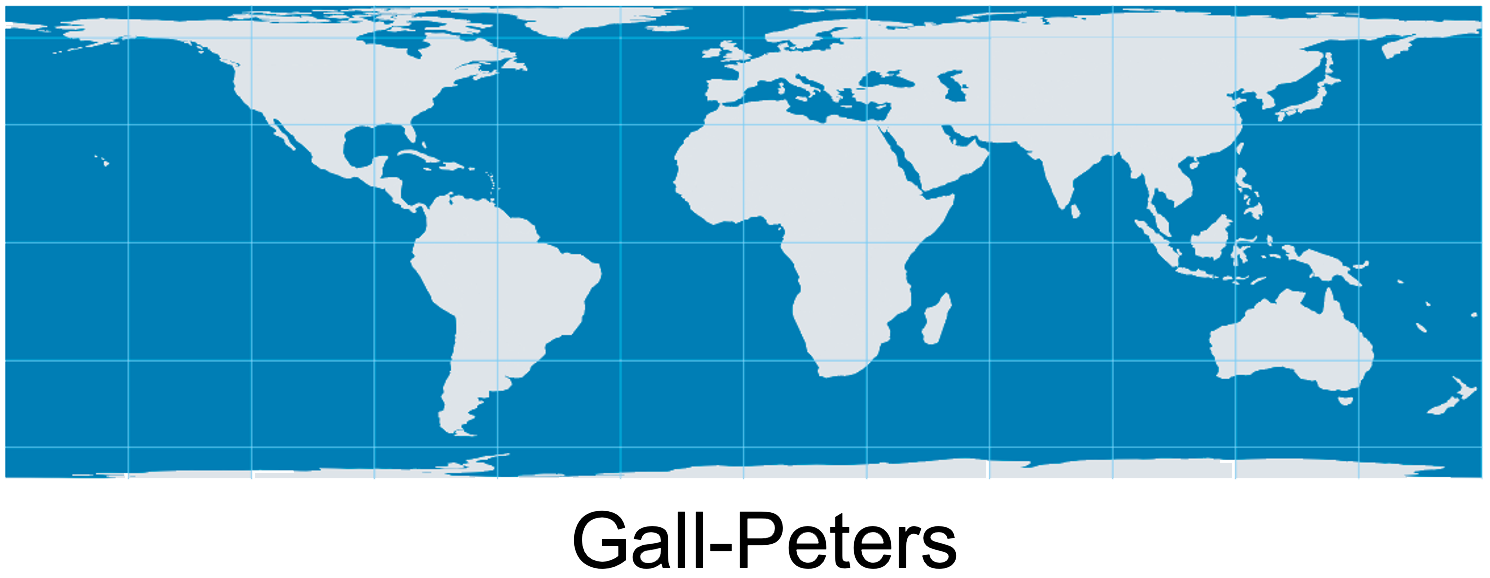
Équivalence (Gall-Peters)
Conserve les surfaces
Les aires représentées sur la carte sont proportionnelles à celles du monde réel.
- Crucial en géographie politique, démographie, économie
- Les formes peuvent être allongées, déformées ou aplaties

Équidistance (Équidistante azimutale)
Conserve les distances
Elle conserve les distances depuis le point central, mais pas entre deux points quelconques sur la carte.
- Utile pour les vols directs, les cartes radiales, les analyses de proximité
- Ne préserve pas les formes ni les surfaces globalement
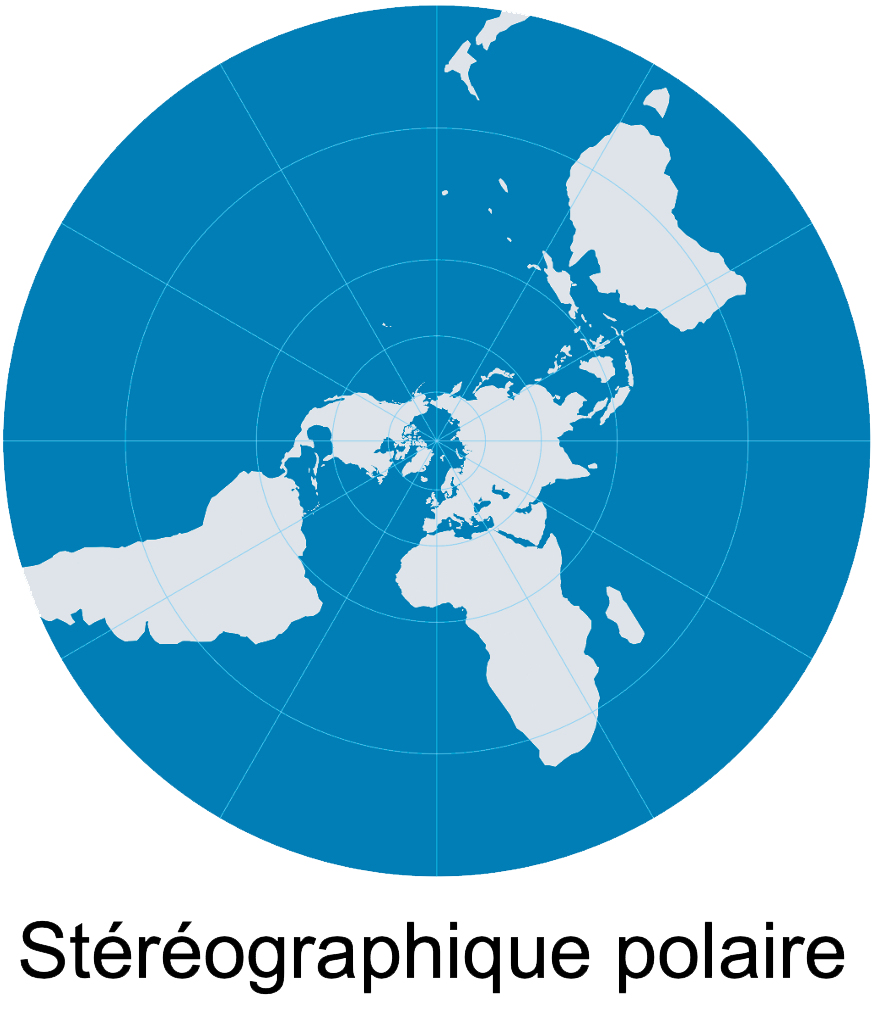
Azimutale (Stéréographique polaire)
Conserve les directions
Les directions exactes à partir d’un point central sont conservées, mais les angles locaux ne sont fidèles qu’à ce point. La forme des objets s’éloignant du centre est donc progressivement déformée.
- Pratique pour les routes aériennes, les cartes satellites, les vues polaires
- La précision diminue hors du point central
Laquelle est la plus courante ?
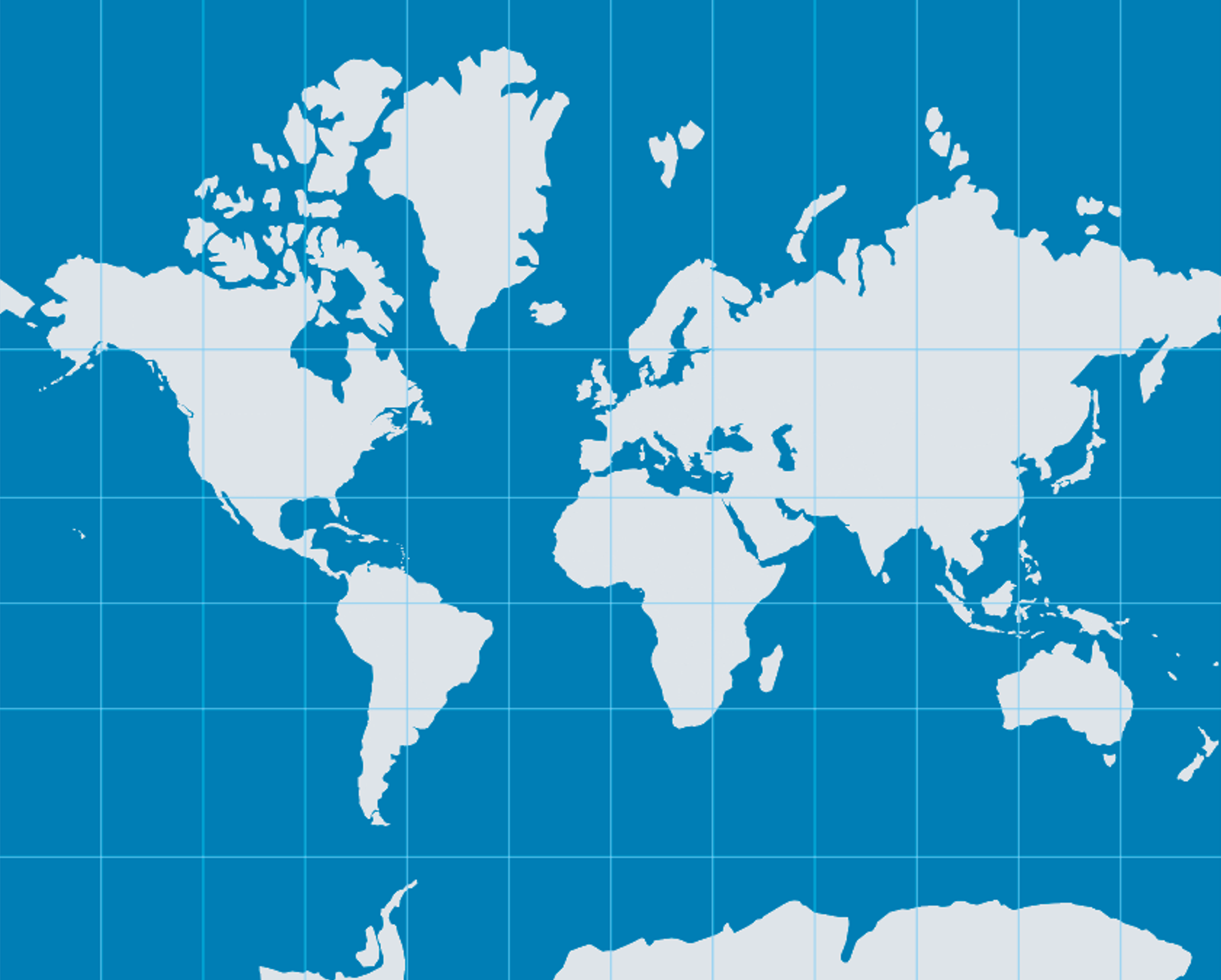
Mercator et Google Maps
Des services comme Google Maps utilisent une variante de Mercator, mais cette projection déforme fortement les surfaces, surtout en s’éloignant de l’équateur. Par exemple, le Groenland y semble aussi grand que l’Afrique, alors qu’il est 14 fois plus petit. Elle donne ainsi une image faussée de l’importance spatiale des régions situées en latitude élevée.
Cette déformation est spectaculaire à petite échelle (c’est-à-dire sur les cartes du monde ou des continents), mais elle devient quasiment imperceptible à grande échelle, lorsqu’on cartographie un territoire restreint, comme une ville ou une région.
La projection de Mercator, conçue en 1569, est une projection cylindrique conforme. Elle a été pensée pour la navigation maritime : grâce à sa propriété de conservation des angles, les loxodromies (routes à cap constant) y apparaissent comme des lignes droites. C’est ce qui en a fait la référence pour les cartes marines pendant des siècles.
Quelle projection pour les petits territoires?
Pour des cartes encore plus précises sur de petits territoires, on utilise souvent des projections locales adaptées, conçues pour limiter au maximum les déformations dans une zone bien définie. C’est le cas des systèmes Universal Transverse Mercator (UTM) et Modified Transverse Mercator (MTM).
Le système UTM divise le globe en 60 zones longitudinales de 6° de large chacune. À l’intérieur de chaque zone, on utilise une projection transverse cylindrique conforme, centrée sur un méridien, ce qui permet de maintenir une très bonne précision sur les distances et les formes locales. C’est le système utilisé dans la majorité des cartes topographiques modernes.
Nos cartes du Québec
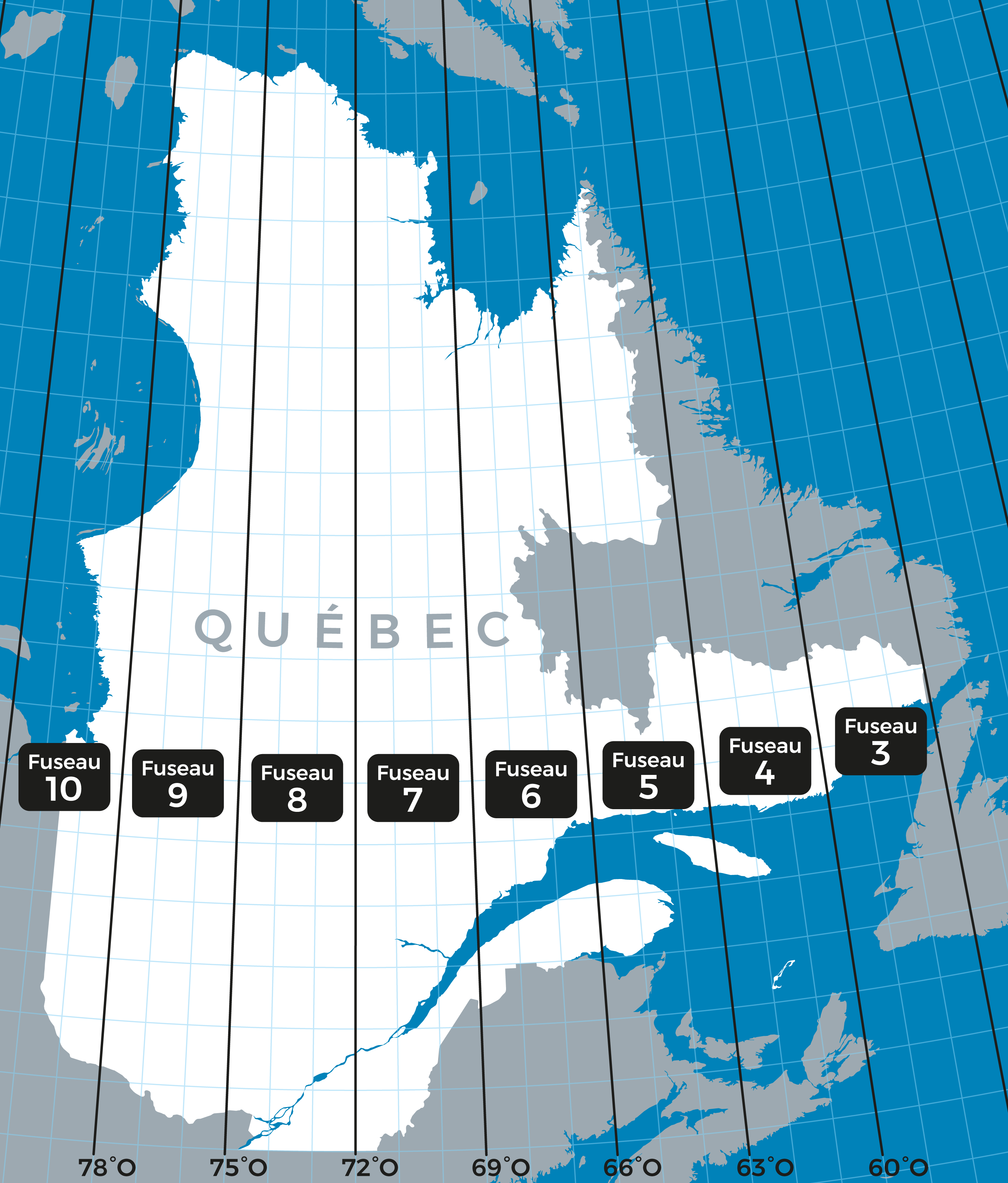
Au Québec, on préfère souvent le système MTM, qui fonctionne sur le même principe UTM, mais avec des zones plus étroites de 3° de longitude, pour encore plus de précision. Chaque bande MTM est associée à un faux méridien central, et est adaptée à la géométrie particulière du territoire québécois, notamment dans les relevés cadastraux, l’aménagement du territoire et les travaux d’ingénierie.
Ces systèmes ne sont pas conçus pour représenter le monde entier, mais ils sont excellents pour la cartographie détaillée à grande échelle (par exemple : une ville, une région, un corridor d’infrastructure). C’est un exemple parfait de projection optimisée pour un usage très localisé, avec des paramètres calibrés selon la position géographique.
Pour les cartes du Canada
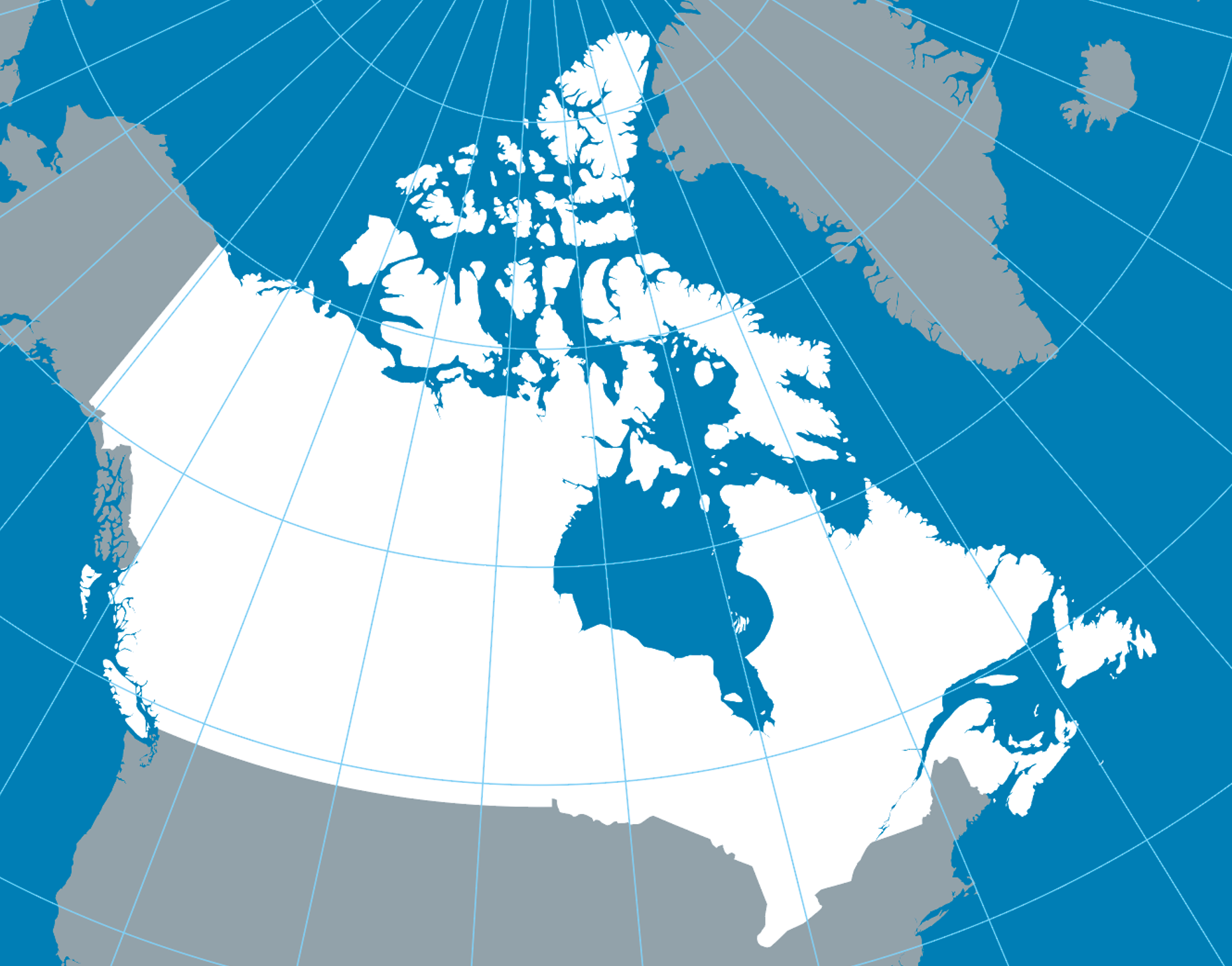
Contrairement à Mercator, la projection conique conforme de Lambert est idéale pour les régions étendues d’est en ouest. Elle est largement utilisée au Canada, notamment pour la cartographie du Québec, de l’Ontario ou des provinces de l’Ouest.
Elle conserve les angles locaux, ce qui garantit une représentation fidèle des formes à l’échelle régionale, tout en limitant les distorsions.
Parallèles et méridiens : une grille pour comprendre
Les méridiens sont les lignes nord-sud, perpendiculaires à l’équateur.
Les parallèles sont les cercles horizontaux parallèles à l’équateur, correspondant aux latitudes.
Ces lignes forment la grille géographique sur laquelle s’appuie toute projection.
Une projection n’est jamais neutre
Chaque projection est un choix en fonction de l’ intention :
- Faciliter la navigation
- Respecter les superficies
- Produire une carte esthétiquement équilibrée
Mais parfois, ces choix renforcent un imaginaire géopolitique. Mercator, par exemple, a longtemps dominé les manuels scolaires, plaçant l’Europe au centre et donnant aux pays du Nord une taille exagérée. À l’inverse, la projection de Peters, plus fidèle aux superficies, a été promue pour souligner les inégalités de représentation.



