Projection cylindrique
Comme si l’on enroulait un cylindre autour du globe, tangent à l’équateur ou à un autre parallèle.
Projection conique
La Terre est projetée sur un cône qui touche un ou deux parallèles (ex : Lambert conforme).
Projection plane (azimutale)
La projection se fait sur un plan tangent (ou sécant) à un point, souvent centré sur un pôle ou un point stratégique.
Conformité (Conserve les formes locales et les angles)
Préserve fidèlement les formes des objets à petite échelle,
grâce au respect des angles locaux
- Idéal pour les cartes côtières, marines, topographiques
- Les surfaces peuvent être très exagérées, surtout près des pôles
Équivalence (Conserve les surfaces)
Les aires représentées sur la carte sont proportionnelles à celles du monde réel.
- Crucial en géographie politique, démographie, économie
- Les formes peuvent être allongées, déformées ou aplaties
Équidistance (Conserve les distances)
Elle conserve les distances depuis le point central, mais pas entre deux points quelconques sur la carte.
- Utile pour les vols directs, les cartes radiales, les analyses de proximité
- Ne préserve pas les formes ni les surfaces globalement
Azimutale (Conserve les directions)
Les directions exactes à partir d’un point central sont conservées, mais les angles locaux ne sont fidèles qu’à ce point. La forme des objets s’éloignant du centre est donc progressivement déformée.
- Pratique pour les routes aériennes, les cartes satellites, les vues polaires
- La précision diminue hors du point central
La projection Mercator : conforme, utile, mais trompeuse
à petite échelle
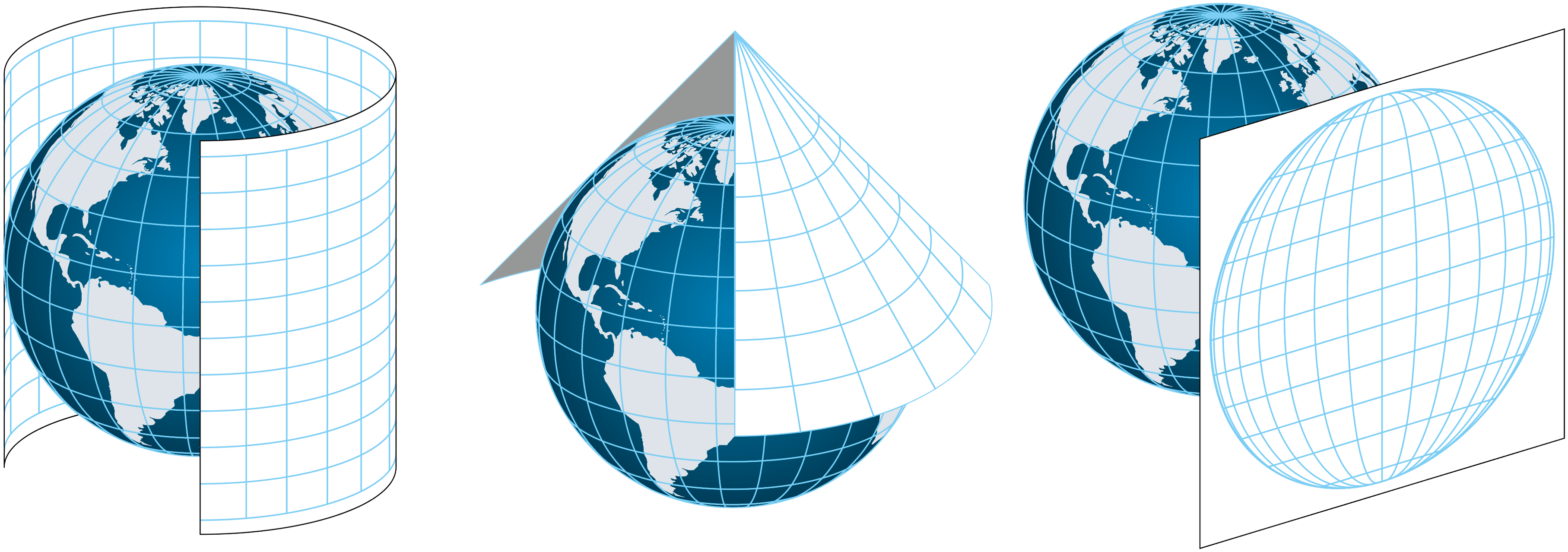
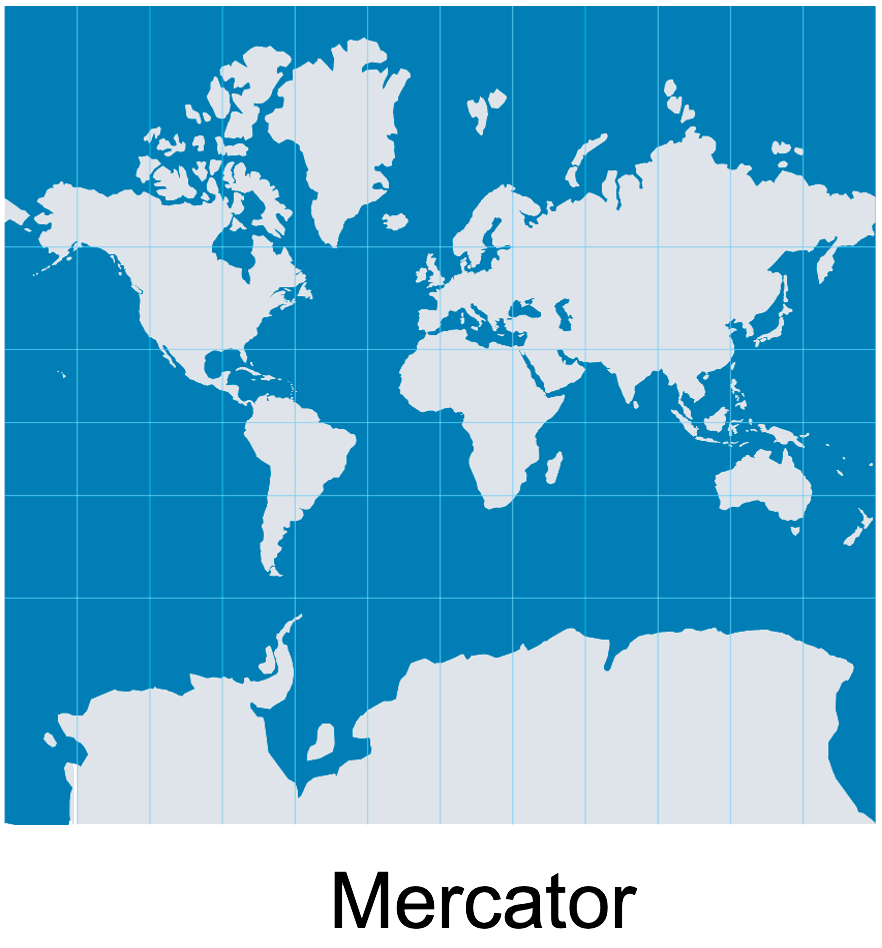
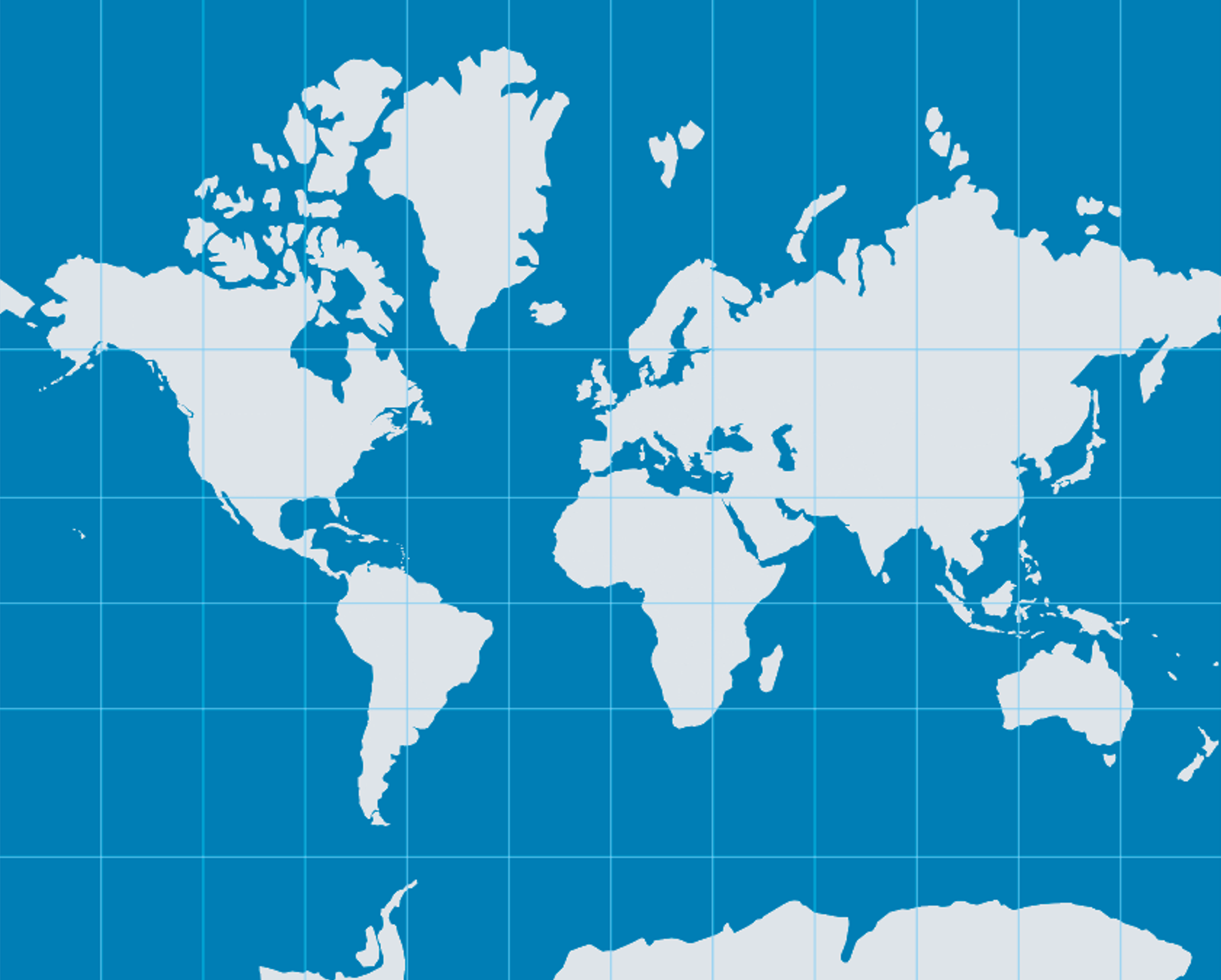La projection de Mercator, conçue en 1569, est une projection cylindrique conforme. Elle a été pensée pour la navigation maritime : grâce à sa propriété de conservation des angles, les loxodromies (routes à cap constant) y apparaissent comme des lignes droites. C’est ce qui en a fait la référence pour les cartes marines pendant des siècles.
Mais cette projection déforme fortement les surfaces, surtout en s’éloignant de l’équateur. Par exemple, le Groenland y semble aussi grand que l’Afrique, alors qu’il est 14 fois plus petit. Elle donne ainsi une image faussée de l’importance spatiale des régions situées en latitude élevée.
Cette déformation est spectaculaire à petite échelle (c’est-à-dire sur les cartes du monde ou des continents), mais elle devient quasiment imperceptible à grande échelle, lorsqu’on cartographie un territoire restreint, comme une ville ou une région.
C’est pourquoi des services comme Google Maps utilisent une variante de Mercator : à l’échelle locale, la conformité angulaire permet de conserver les formes et orientations, et les distorsions de surface sont négligeables.
Pour des cartes encore plus précises sur de petits territoires, on utilise souvent des projections locales adaptées, conçues pour limiter au maximum les déformations dans une zone bien définie. C’est le cas des systèmes UTM (Universal Transverse Mercator) et MTM (Modified Transverse Mercator).
Le système UTM divise le globe en 60 zones longitudinales de 6° de large chacune. À l’intérieur de chaque zone, on utilise une projection transverse cylindrique conforme, centrée sur un méridien, ce qui permet de maintenir une très bonne précision sur les distances et les formes locales. C’est le système utilisé dans la majorité des cartes topographiques modernes.
Au Québec, on préfère souvent le système MTM, qui fonctionne sur le même principe, mais avec des zones plus étroites de 3° de longitude, pour encore plus de précision. Chaque bande MTM est associée à un faux méridien central, et est adaptée à la géométrie particulière du territoire québécois, notamment dans les relevés cadastraux, l’aménagement du territoire et les travaux d’ingénierie.
Ces systèmes ne sont pas conçus pour représenter le monde entier, mais ils sont excellents pour la cartographie détaillée à grande échelle (par exemple : une ville, une région, un corridor d’infrastructure). C’est un exemple parfait de projection optimisée pour un usage très localisé, avec des paramètres calibrés selon la position géographique.
Projection de Lambert conforme : idéale pour les cartes nationales au Canada
Contrairement à Mercator, la Lambert conforme conique est une projection conique conforme, idéale pour les régions étendues d’est en ouest. Elle est largement utilisée au Canada, notamment pour la cartographie du Québec, de l’Ontario ou des provinces de l’Ouest.
Elle conserve les angles locaux, ce qui garantit une représentation fidèle des formes à l’échelle régionale, tout en limitant les distorsions.
